Q3 算数オリンピックトライアル1
ももこさんが算数の試験を5回受けました。下の父親との会話を読んで問いに答えなさい。
ももこ:おとうさん、算数の点数が試験を受けるたびに高くなったよ!
父親 :すごいじゃないか!しかも上がっている点数も、回を追うごとに大きくなってる。
最後の点数は最初の点数の2倍くらいあるじゃないか!
ももこ:勉強頑張ったからね!でもさすがに2倍はいかないよ。
父親 :そうだね。おや、点数の数字はすべて異なる数だね。
ももこ:本当だ!こんな偶然もあるんだね。
ももこさんの1回目の点数と5回の試験の平均点の組み合わせを1つ求めなさい。
5回のテストの点数の条件をまとめると次のようになります.
条件① 点数は受けるたびに高くなる.
条件② 上がっている点数は回を追うごとに大きくなる.
条件③ 5回目の点数は1回目の点数の2倍未満.
条件④ 点数の数字はすべて異(こと)なる数.
条件②より1回目と5回目の点数の差は最低でも 1+2+3+4=10点 なので1回目の点数が1けたの場合は,条件③を満たしません.よって1回目の点数は2けたです.
1回目の点数が2けたであること,そして条件③から1回目の点数は30点台か40点台です.
1回目が30点台のときは条件③より5回目は70点台なので次のようになります.

このとき残りの数字 0 , 1 , 2 , 8 , 9 をどのように入れても,条件②を満たしません.
1回目が40点台のときは条件③より5回目は80点台か90点台,そして条件②を含(ふく)めると次の2通りが考えられます.
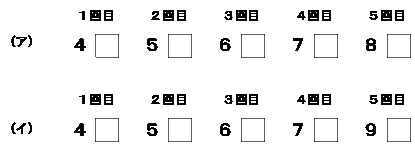
(ア)のとき条件②を満たすように一の位を入れると49 , 52 , 60 , 71 , 83 や 49 , 53 , 61 , 70 , 82 があてはまります.一の位の数字を入れかえただけなのでどちらも平均点は同じになります.
平均点は (49+52+60+71+83)÷5=63点
(イ)のとき条件②を満たすように一の位を入れると48 , 52 , 60 , 71 , 93 や 48 , 53 , 61 , 70 , 92 などがあてはまります.(※ 他にも8通りの入れ方があります.)
一の位の数字を入れかえただけなのでどちらも平均点は同じになります.
平均点は (48+52+60+71+93)÷5=64.8点
答え: (49点 , 63点) , (48点 , 64.8点)
過去の投稿
- 2019年 (7)

