2019/3/8
Q4 算数オリンピックトライアル2
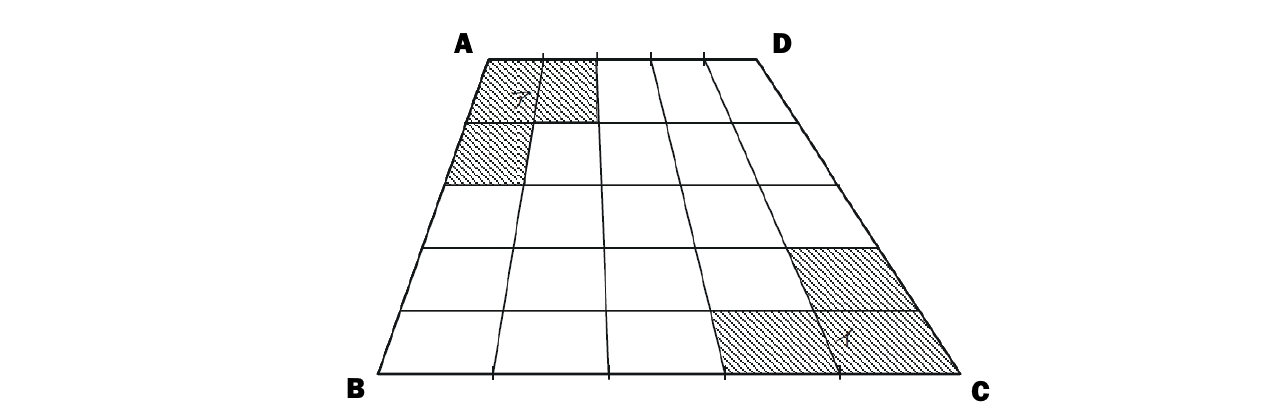
図のように、台形ABCDの各辺を五等分し、辺ADと辺BCの等分した点どうし、
辺ABと辺DCの等分した点どうしを線で結びました。このとき、辺ABと辺DCの等分した点どうしで結んだ線はすべて辺 AD, BC と
平行になりました。また、斜線部アの面積は49㎠,斜線部イの面積は134㎠となりました。
このとき、台形ABCDの面積を求めなさい

答えを見るには、をクリックしてください。
それぞれの部分の面積を図1の
ように P, Q, R, S, T とします.
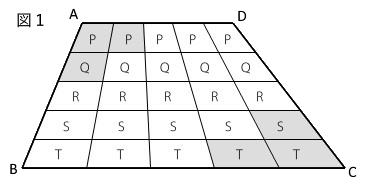
それぞれの部分の面積を図1の
ように P, Q, R, S, T とします.
このとき
P×2+Q=49 式①
S+T×2=134 式②

式①+式② より P×2+Q+S+T×2=183 式③
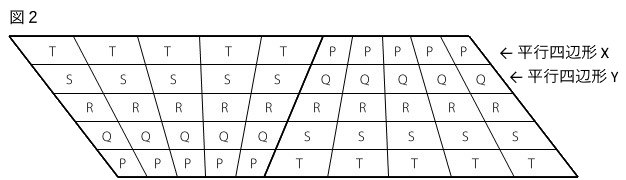
次に台形ABCDをひっくり返してくっつけた図2のような形を考えます.

このとき
平行四辺形Xと平行四辺形Yの面積は等しいので P×5+T×5=Q×5+S×5
左右を5で割(わ)ると P+T=Q+S となります.
式③の Q+S を P+T に置きかえると P×3+T×3=183
左右を3で割ると P+T=61 となります.
よって
(平行四辺形Xの面積)=P×5+T×5=(P+T)×5=61×5=305cm2 なので
(図2の面積)=305×5=1525cm2
台形ABCDは図2の半分なので
(台形ABCDの面積)=1525÷2=762.5cm2
答え:762.5cm2
過去の投稿
- 2019年 (7)

