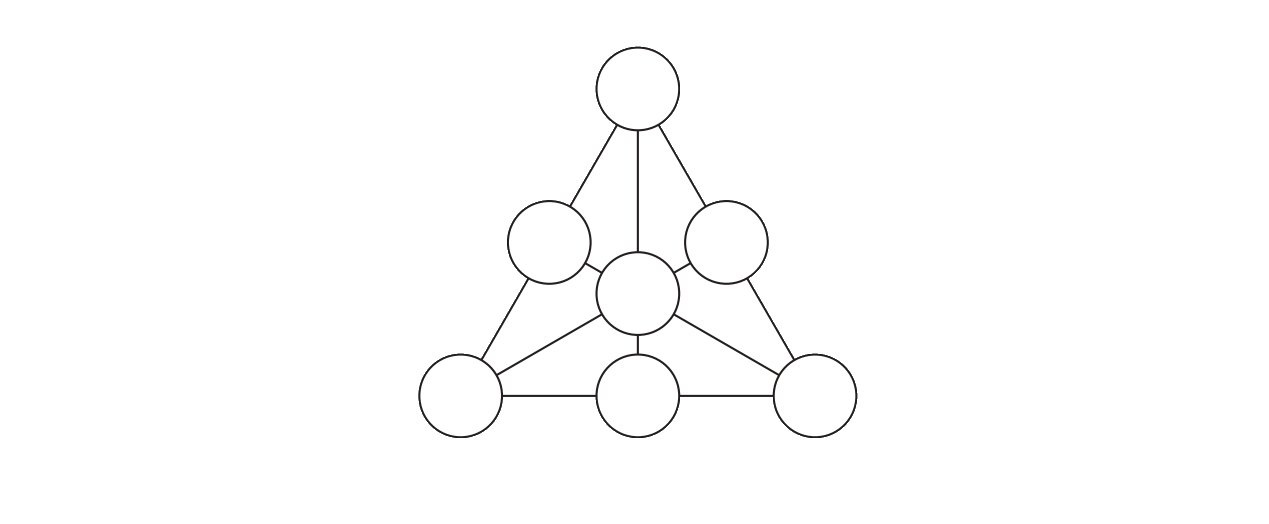
〇が7個なのに対して，20以下の素数は2，3，5，7，11，13，17，19の8個です．2以外の素数はすべて奇(き)数(すう)であり，偶(ぐう)数(すう)＋奇数＋奇数＝偶数なので，2は使えないことになります．
これにより，使う7個の整数は3，5，7，11，13，17，19になります．
また，7個の〇のうち，外側の大きな三角形の各辺の真ん中にある3個の〇は2本の直線上にあり，その他の4個の〇は3本の直線上にあります．

一方，3個の和が素数になる組み合わせは，

①(3，5，11)，②(3，7，13)，③(3，7，19)，④(3，11，17)，
⑤(5，7，11)，⑥(5，7，17)，⑦(5，7，19)，⑧(5，11，13)，⑨(5，13，19)，⑩(5，17，19)
⑪(7，11，13)，⑫(7，11，19)，⑬(7，13，17)，⑭(7，17，19)，
⑮(11，13，17)，⑯(11，13，19)，⑰(11，17，19)

の17通りです．

このうち，3がふくまれるのは①～④の4通りですが，このうち①と④，②と③はどちらも共通な2個の素数をふくんでいるので，同時に使うことができません．つまり，①～④の中で可能な組み合わせは，

ア.①(3，5，11)と②(3，7，13)　 イ.①(3，5，11)と③(3，7，19)
ウ.②(3，7，13)と④(3，11，17)　エ.③(3，7，19)と④(3，11，17)

の4通りです．いずれも，3がふくまれる組み合わせは2通りしか選べないので，3は外側の大きな三角形の各辺の真ん中にある3個の〇のどれかに入ることがわかります．
実際に成立するのは，ア，イ，エの3通りです．3を下の段の中央に置いて，回転や反転したものを除(のぞ)いて調べると，下記の12通りあります．

これらを反転したり，回転したりすると，(12×3×2＝)72通りあり，そのいずれかを書けば正解となります．

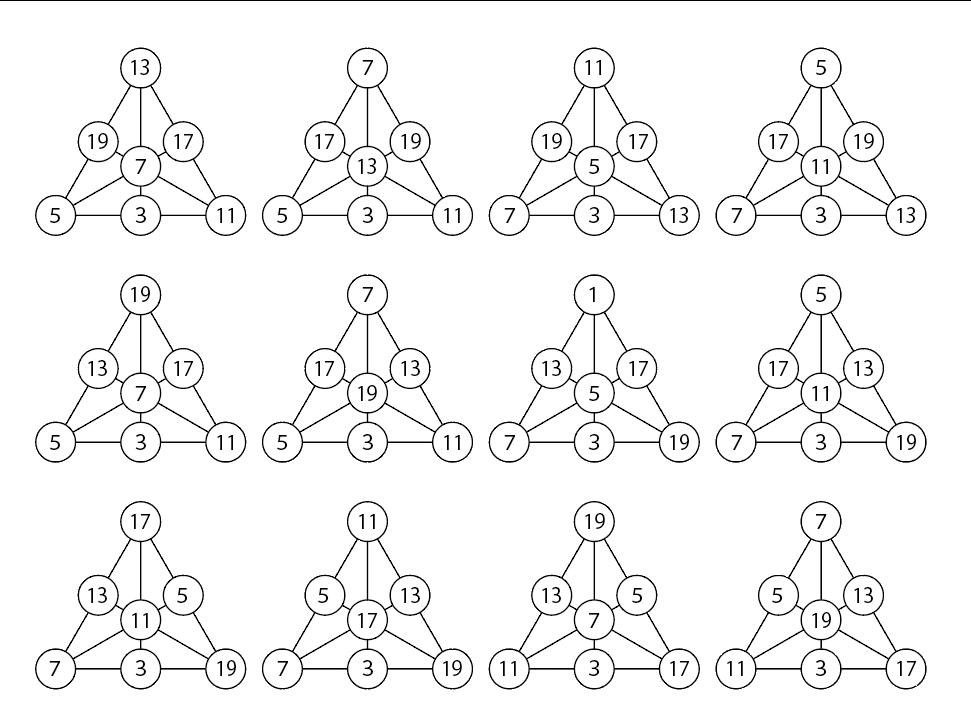
答え：72通りのうち1通りを書けば正解